SILO 6.1 (DRAFT)Year 6, Term 1: NanotechnologyFocus: Ratios Scope
and sequence: Calibration, Exponents, Ratios,
Scales
|
|
Learning
intention: Students
convert between metric units of length, mass and capacity
and make relevant connections to the properties of water.
|
|
|
Overview: Nanotechnology
involves the manipulation of matter on a near-atomic scale which
might suggest that this is beyond what Year 6 students can
investigate, but certain principles such as the ratio between
surface area and volume are manageable and relevant for this age
group. These concepts are scaffolded by looking at the metric
system, calibration and various scales used in science, namely;
ordinal, linear and logarithmic.
|
|
|
NSW Syllabus
|
Australian Curriculum
(version 9.0)
|
|
"A student selects and uses the
appropriate unit to estimate, measure and calculate volumes and
capacities." (MA3-3DS-02)
|
"Students learn to convert between
common metric units of length, mass and capacity; choose and use
decimal representations of metric measurements relevant to the
context of a problem." (AC9M6M01)
|
Introduction to nanotechnology
A nanometre is one billionth of a metre (i.e., one millionth of a millimetre).
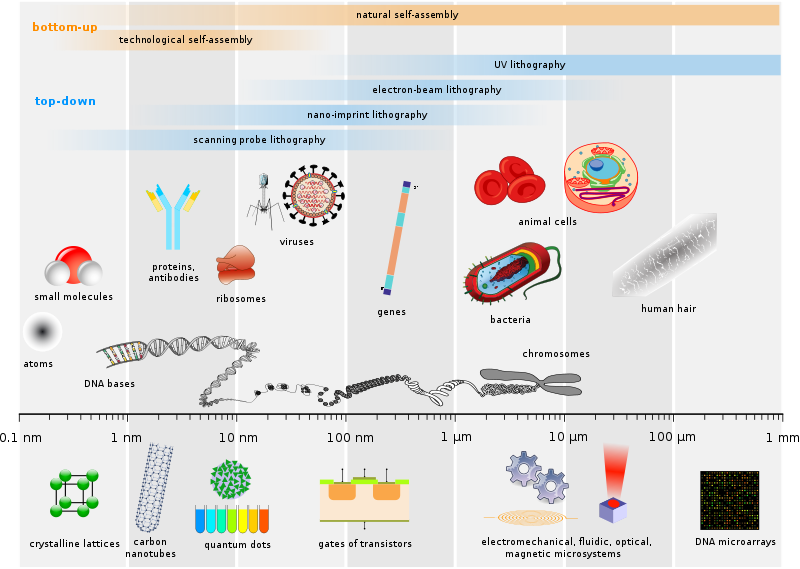
(CC BY-SA 2.5 Source: https://commons.wikimedia.org/wiki/File:Biological_and_technological_scales_compared-en.svg)
This video (3:29) explains some of the ways in which
nanotechnology is at the cutting edge of science and technology.
Exploring the ratio of surface area to volume
The main thing to note here is that the ratio of surface
area to volume is not fixed as shown in the figure below.
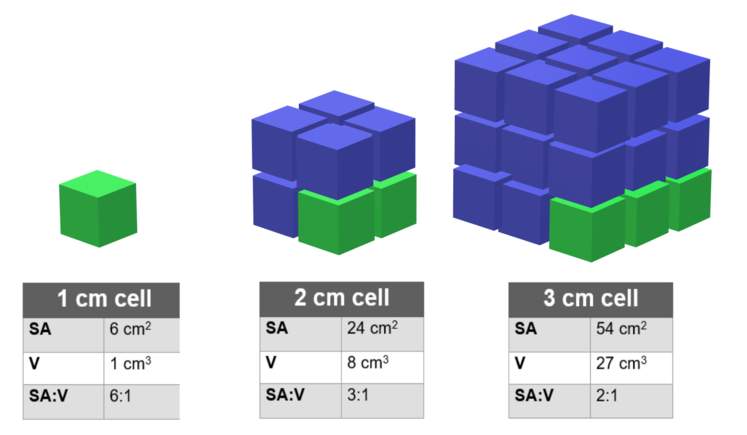
https://commons.wikimedia.org/wiki/File:Unit_cell_for_SA_to_V_ratio_with_tables.png
There are many examples of this principle in nature. For example:
- Chewing food into smaller pieces aids digestion as the surface area is increased while the volume remains the same.
- Your fingers are the first parts of your body to get cold as they have a high ratio of surface area to volume.
- Elephants have large ears to help them keep cool as their ears also have a high ratio of surface area to volume.
The ratio of surface area to volume can also be seen in everyday phenomena. For example, when building a fire it is common to use small pieces of wood first which is know as kindling. Because the kindling is small, it has a larger surface area compared to its volume.
The following graph shows the surface area (A) against volume (V) of the five Platonic solids and a sphere. Note the following:
- The surface area decreases for rounder shapes.
- The surface-area-to-volume ratio decreases with increasing volume.
- The intercepts with the dashed lines show that when the volume increases 8 (2³) times, the surface area increases 4 (2²) times.
The following video (2:26) contains two examples of how nanotechnology
is being used in the field of medical research to fight cancer.
The logical behind the metric system
The metric system is logical because it is uses the same base 10 system which we use with our number. In addition to this there are some important things to know about the properties of water and how these how been used to calibrate the Celsius scale for temperature. Water freezes at 0 degrees Celsius and boils at 100 degrees.
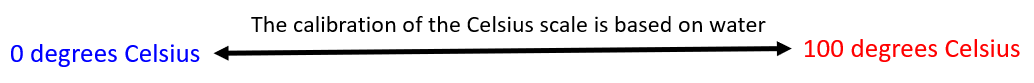
- The temperature inside a refrigerator is generally set around 4 degrees Celsius.
- Human bodies are generally around 37 degrees Celsius.
The metric system also uses water as the basis for quantifying volume and mass. This is not coincidental but by design.

Types of scales
Ordinal scales
An ordinal scale has a non specified degree of variation. In other words, the scale is somewhat arbitrary. An example is the Mohs scale of mineral hardness introduced in 1822 by the German geologist and mineralogist Friedrich Mohs.
 |
What do you notice when you compare the 'Mohs hardness' numbers with the 'Absolute hardness' numbers?Is there a direct correlation?
|
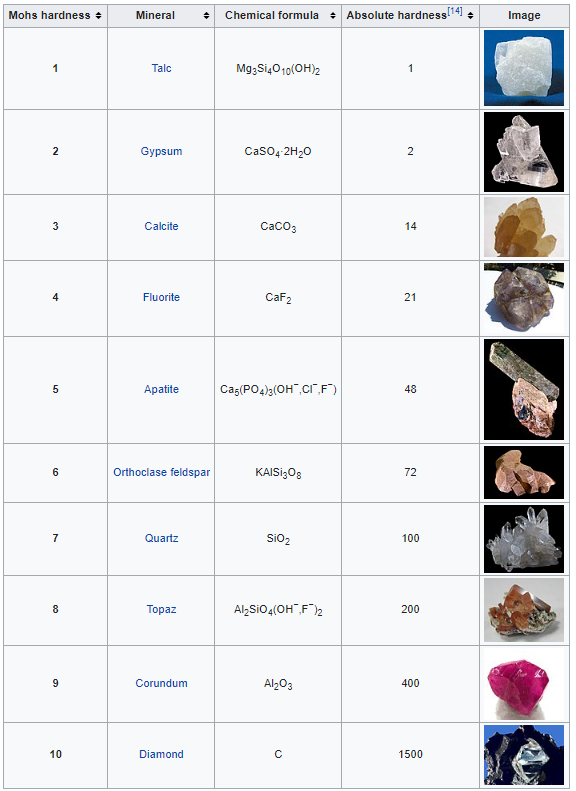
Linear scales
A linear scale has a specified degree of variation. In
other words, there is a direct mathematical correlation along the
scale due to the way that it has been calibrated. An example is the
Celsius scale.
Logarithmic scales
In a logarithmic scale, each interval is increased by a factor of the base of the logarithm, which is often a multiple of 10. Examples of common logarithmic scales are pH (to measure acidity), decibels (sound intensity), and the Richter scale (earthquakes).

 |
Review the information provided in the article at https://www.abc.net.au/news/2015-11-19/tropical-cyclone-categories-explained/6956092. Are cyclone categories ordinal, linear or logarithmic?
|
Calibration
Calibration is the process of configuring an instrument
to improve the accuracy of measurements and readings. The following
video (1:39) uses calibration to improve the accuracy of a digital
compass.
Combinations and permutations
In mathematics, when the order doesn't matter it is a combination. When the order does matter it is a permutation. A permutation is an ordered combination.This means that what are commonly called combination locks are really permutation locks.
Exponents
Exponents are not part of the curriculum in primary school but they can be discussed and informally introduced in various ways.
 |
How many permutations are there with a six-character number plate? |
(Answer is at the bottom of this page)

The inverse square law
The inverse square law describes how the intensity of a physical quantity radiating from a point source decreases with distance. The intensity is inversely proportional to the square of the distance from the source. This principle applies to various physical phenomena including light, sound, gravity and radiation. The following image shows how the intensity at double the distance is 1/4 of its original value and 1/9 when the distance is three times further.
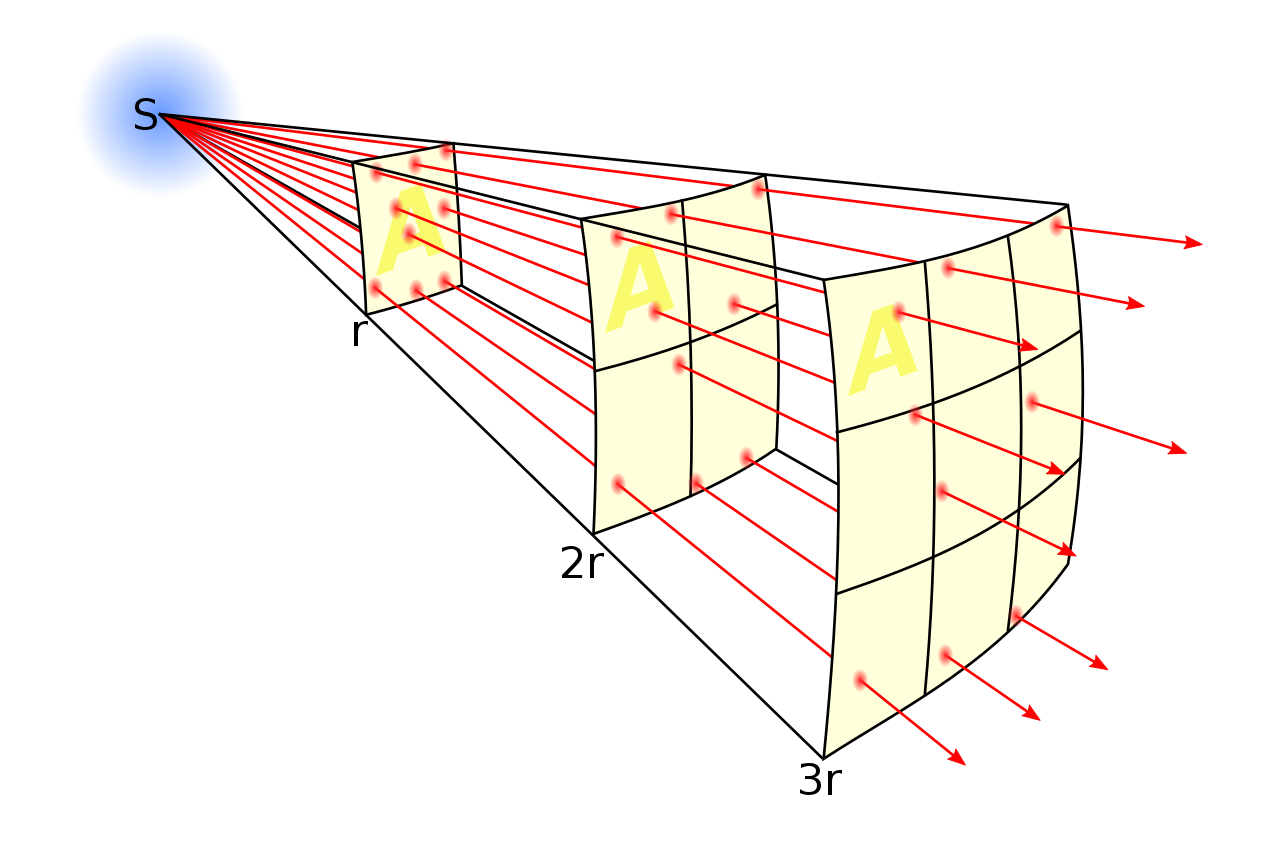
Static electricity
This video (2:08) includes a vivid example of how water
molecules are polarised.
 |
How
might the inverse square law affect the static
electricity and water experiment?
|
The International system of units
The International System of Units (abbreviated as SI) is based on the metric system and is the world's most widely used system of measurement. It is the only system of measurement with official status in nearly every country in the world. The seven SI base units are:
| Symbol | Name | Quantity |
| s |
second | time |
| m |
metre | length |
| kg |
kilogram | mass |
| A |
ampere | electric current |
| K |
kelvin | thermodynamic temperature |
| mol |
mole | amount of substance |
| cd |
candela | luminous intensity |
The following image is way beyond what primary school students are expected to know but it is a really good visualisation of how the SI units are related to one another.It is an arrangement of the principal measurements in physics based on the mathematical manipulation of length, time and mass.
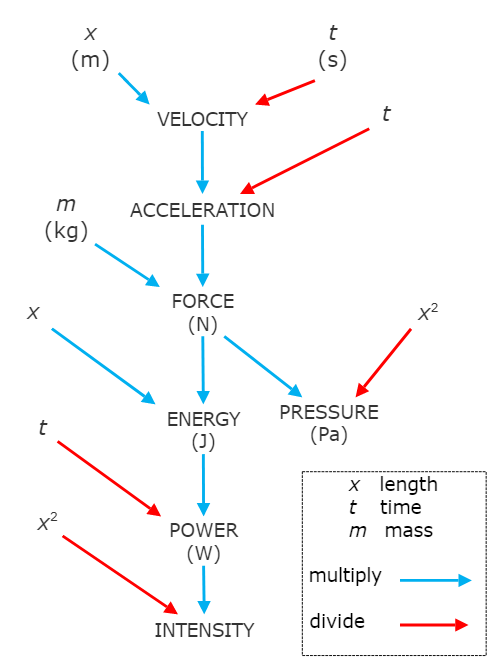
(Image source https://en.wikipedia.org/wiki/International_System_of_Units#/media/File:Physics_measurements_SI_units.png)
Moderated self-assessment
Discussions with students around the key components of conceptual topics and how they fit together can generate insights into student achievement.
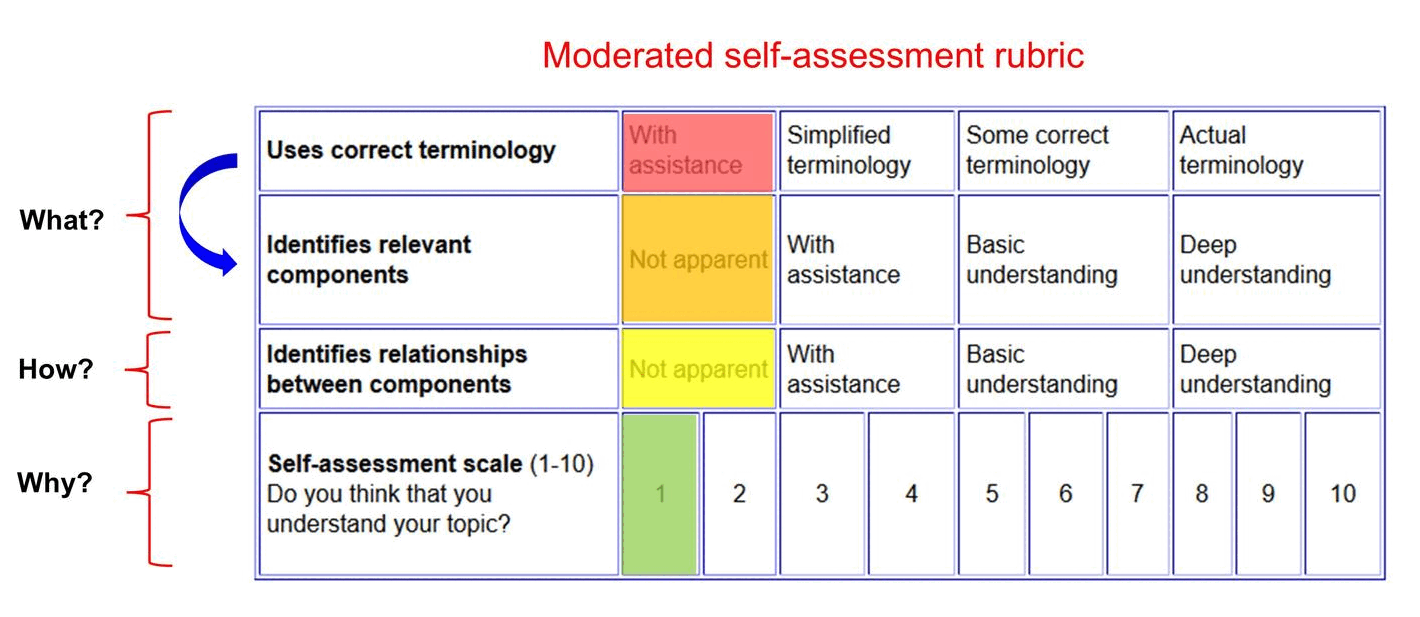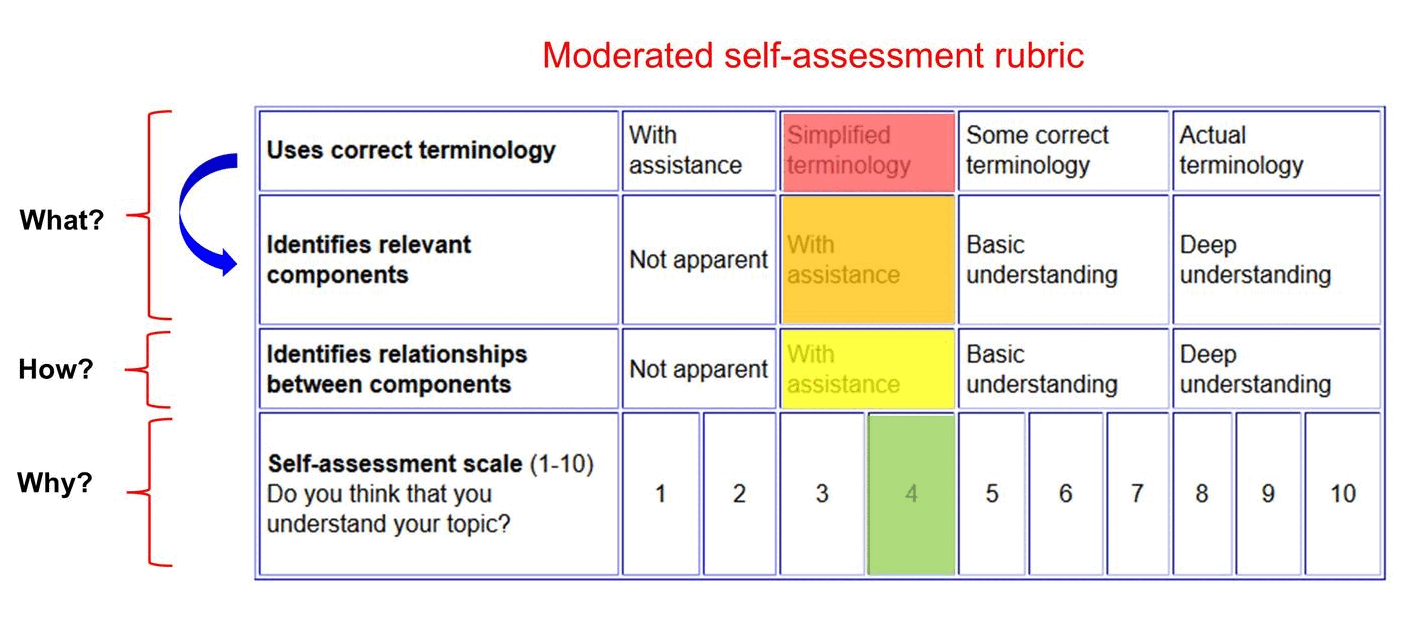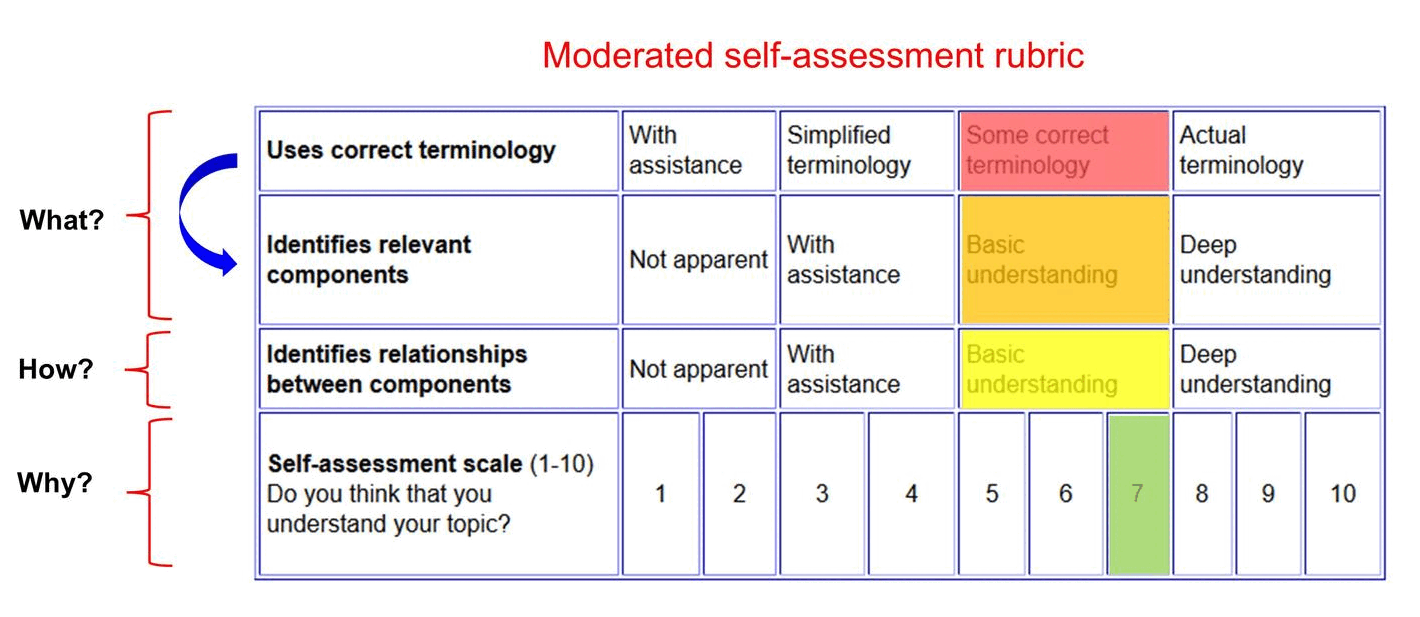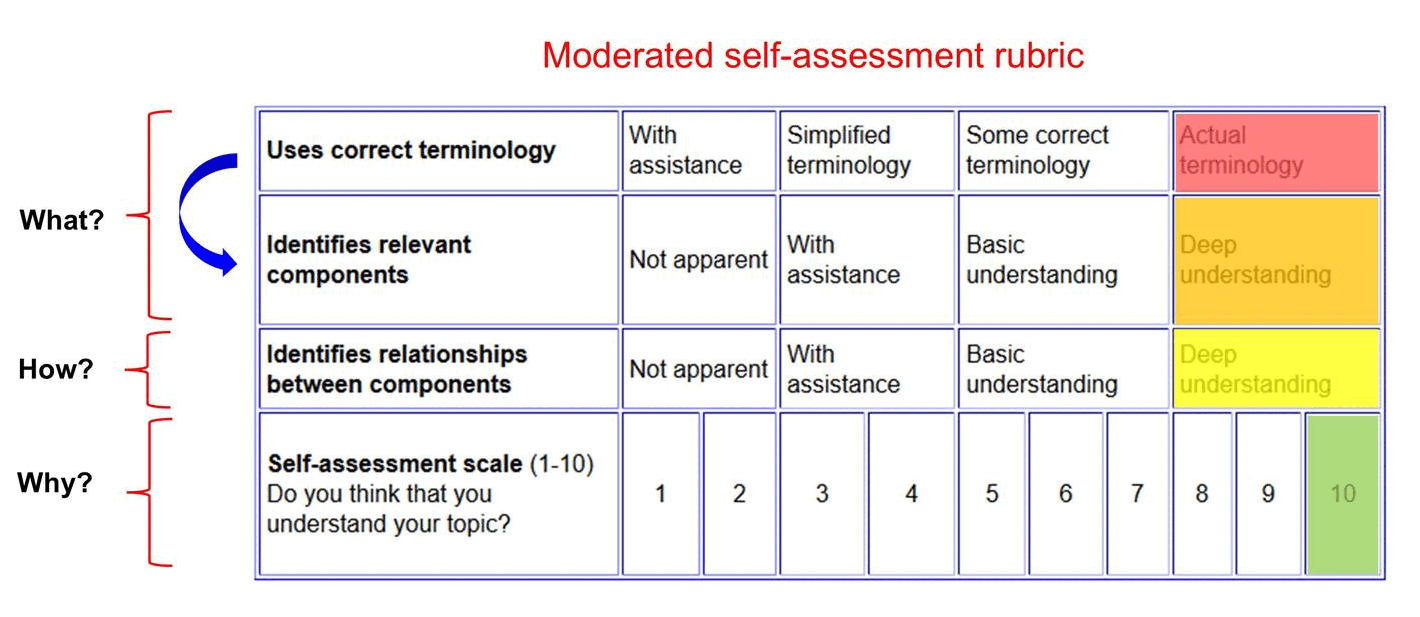
------------------
Answer to the exponents question about permutations with six character number plates:

------------------

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Main menu